Met de gemeenteraadsverkiezingen in aantocht komt de aloude vraag weer boven: “hoe wordt het aantal zetels ook alweer berekend?”. Dit is niet simpel afronden en er zijn subtiele verschillen tussen de verschillende soorten verkiezingen en hoeveel zetels er te verdelen zijn.
Voor alle soorten verkiezingen geldt dat het totaal aantal stemmen wordt gedeeld door de hoeveelheid zetels die er te verdelen zijn, dit is de kiesdeler. Vervolgens wordt het aantal stemmen dat elke lijst heeft gehaald gedeeld door de kiesdeler. Dit getal wordt naar beneden afgerond en is het aantal volle zetels dat een lijst krijgt. Omdat er naar beneden wordt afgerond zijn er altijd nog wat zetels over, de restzetels. Er zijn twee systemen om restzetels te verdelen, afhankelijk van het aantal zetels van de raad in kwestie. Bij 19 of meer zetels wordt het systeem van grootste gemiddelden gebruikt, anders het systeem van grootste overschotten.
De twee systemen worden hieronder verder uitgelegd. Uit gewoonte gebruik ik een punt als decimaalteken, niet een komma. 1.999 is dus bijna 2, niet bijna 2000. Ik zal proberen zoveel mogelijk te voorkomen dat hier verwarring over kan ontstaan.
Grootste gemiddelden
Als er 19 of meer zetels te verdelen zijn (zoals in het Europees Parlement, Eerste en Tweede Kamer, Provinciale Staten en de meeste Gemeenteraden) dan worden restzetels verdeeld met het systeem van grootste gemiddelden. Na het verdelen van de volle zetels (z) heeft elke partij een aantal stemmen per zetel (S/Z). Dan wordt voor elke partij wordt uitgerekend hoeveel stemmen per zetel ze zouden hebben als 1 extra zetel zouden krijgen (S/(Z+1)). Het aantal toegekende zetels plus de extra zetel is het aantal virtuele zetels. De partij met het hoogste gemiddelde krijgt de extra zetel. Als er meer restzetels te verdelen zijn dan wordt het aantal stemmen per zetel opnieuw uitgerekend, inclusief de eerder toegewezen restzetel(s).
| Partij |
Stemmen |
Zetels |
s/z |
s/(z+1) |
Zetels |
% stemmen |
% zetels |
| A |
101 |
9 |
11.22 |
10.1 |
10 |
84.2% |
90.9% |
| B |
19 |
1 |
19.00 |
9.5 |
1 |
15.8% |
9.1% |
Tabel 1: Rekenvoorbeeld van grootste gemiddelden
Tabel 1 geeft een rekenvoorbeeld. Partij A heeft 101 stemmen, partij B 19. Er zijn 11 zetels te verdelen. De kiesdeler is 120/11 = 10.91. Partij A komt in aanmerking voor 9 volle zetels, partij B voor 1 volle zetel. Het aantal stemmen per zetel (S/Z) voor partij B is veel hoger dan voor partij A. Voor de verdeling van de restzetel wordt echter gekeken naar het gemiddelde met een extra zetel, S/(Z+1). Dit is voor partij A hoger dan voor partij B en deze krijgt dan ook de restzetel toegewezen.
| partij |
s |
z |
s/z |
s/(z+1) |
z |
s/(z+1) |
z |
s/(z+1) |
z |
s/(z+1) |
z |
s/(z+1) |
z |
s/(z+1) |
z |
s/(z+1) |
z |
s/(z+1) |
z |
r |
%s |
%z |
| VVD |
2238351 |
31 |
72205 |
69948 |
32 |
67829 |
32 |
67829 |
32 |
67829 |
32 |
67829 |
33 |
65834 |
33 |
65834 |
33 |
65834 |
33 |
2 |
21.29 |
22.0 |
| PvdA-GL |
1559299 |
22 |
70877 |
67796 |
22 |
67796 |
22 |
67796 |
22 |
67796 |
22 |
67796 |
22 |
67796 |
23 |
64971 |
23 |
64971 |
23 |
1 |
14.83 |
15.3 |
| PVV |
1372941 |
19 |
72260 |
68647 |
19 |
68647 |
20 |
65378 |
20 |
65378 |
20 |
65378 |
20 |
65378 |
20 |
65378 |
20 |
65378 |
20 |
1 |
13.06 |
13.3 |
| SP |
955633 |
13 |
73510 |
68260 |
13 |
68260 |
13 |
68260 |
13 |
68260 |
14 |
63709 |
14 |
63709 |
14 |
63709 |
14 |
63709 |
14 |
1 |
9.09 |
9.3 |
| CDA |
1301796 |
18 |
72322 |
68516 |
18 |
68516 |
18 |
68516 |
19 |
65090 |
19 |
65090 |
19 |
65090 |
19 |
65090 |
19 |
65090 |
19 |
1 |
12.38 |
12.7 |
| D66 |
1285819 |
18 |
71434 |
67675 |
18 |
67675 |
18 |
67675 |
18 |
67675 |
18 |
67675 |
18 |
67675 |
18 |
67675 |
19 |
64291 |
19 |
1 |
12.23 |
12.7 |
| CU-SGP |
575221 |
8 |
71903 |
63913 |
8 |
63913 |
8 |
63913 |
8 |
63913 |
8 |
63913 |
8 |
63913 |
8 |
63913 |
8 |
63913 |
8 |
0 |
5.47 |
5.3 |
| PvdD |
335214 |
4 |
83804 |
67043 |
4 |
67043 |
4 |
67043 |
4 |
67043 |
4 |
67043 |
4 |
67043 |
4 |
67043 |
4 |
67043 |
5 |
1 |
3.19 |
3.3 |
| 50+ |
327131 |
4 |
81783 |
65426 |
4 |
65426 |
4 |
65426 |
4 |
65426 |
4 |
65426 |
4 |
65426 |
4 |
65426 |
4 |
65426 |
4 |
0 |
3.11 |
2.7 |
| Denk |
216147 |
3 |
72049 |
54037 |
3 |
54037 |
3 |
54037 |
3 |
54037 |
3 |
54037 |
3 |
54037 |
3 |
54037 |
3 |
54037 |
3 |
0 |
2.06 |
2.0 |
| FvD |
187162 |
2 |
93581 |
62387 |
2 |
62387 |
2 |
62387 |
2 |
62387 |
2 |
62387 |
2 |
62387 |
2 |
62387 |
2 |
62387 |
2 |
0 |
1.78 |
1.3 |
Tabel 2: De uitslagen van de Tweede Kamerverkiezingen 2017. Er zijn twee lijstverbindingen, tussen PvdA en GroenLinks en tussen ChristenUnie en SGP. De kiesdeler was 70107. Partijen die de kiesdeler niet haalden zijn weggelaten.
Tabel 2 laat de situatie voor de Tweede Kamerverkiezingen 2017 zien. Het is een grote brij van cijfers omdat er meerdere rondes nodig waren voor het verdelen van restzetels. Aan de rechterzijde is de extra kolom R opgenomen, dit is het aantal restzetels dat een partij heeft gekregen.
Grootste overschotten
Als er minder dan 19 zetels te verdelen zijn (zoals bij sommige gemeenteraden) dan worden restzetels verdeeld door het systeem van grootste overschotten. Dit systeem wordt ook gebruikt voor de verdeling van zetels binnen lijstverbindingen (later meer daarover). Eerst wordt bepaald hoeveel volle zetels elke lijst krijgt. Vervolgens wordt het aantal zetels maal de kiesdeler afgetrokken van het aantal stemmen, dit zijn de overschotten. De partijen met de grootste overschotten krijgen de restzetels. Partijen moeten minimaal 75% van de kiesdeler hebben gehaald om in aanmerking te komen voor zo’n restzetel. Elke partij kan op deze manier 1 zetel toegewezen krijgen. Mochten er meer restzetels te vergeven zijn dan wordt daarvoor het systeem van grootste gemiddelden gebruikt. Dit kan gebeuren als er veel partijen zijn die de net niet genoeg stemmen halen voor een (rest)zetel.
| Partij |
Stemmen |
Zetels |
Overschot |
Volgorde |
Zetels |
% stemmen |
% zetels |
| A |
101 |
9 |
2.8 |
2 |
9 |
84.2% |
81.8% |
| B |
19 |
1 |
8.1 |
1 |
2 |
15.8% |
18.2% |
Tabel 3: Rekenvoorbeeld van grootste overschotten
Ook hier een voorbeeld. De uitgangssituatie in Tabel 3 is hetzelfde als in Tabel 1, maar nu wordt het grootste overschot gebruikt om de restzetel te verdelen. Deze is duidelijk hoger voor partij B, die nu de restzetel krijgt.
“Grootste gemiddelden” is nadeling voor partijen met weinig zetels
Het is duidelijk dat de twee rekenmethoden leiden tot verschillende resultaten. In de voorbeelden hierboven krijgt partij A 84% van de stemmen. Met “grootste gemiddelden” krijgen zij 91% van de zetels, met “grootste overschotten” 82% van de zetels. Dit is natuurlijk een voorbeeld met slechts 2 partijen. Bij de Tweede Kamerverkiezingen 2017 verschillen de percentages stemmen en zetels met minder dan 1%. Toch is het systeem van grootste gemiddelden voordelig voor grotere partijen. De 6 grootste lijsten hebben elk een restzetel gekregen (de VVD zelfs 2). Van de 5 kleinste lijsten heeft alleen de PvdD een restzetel gekregen.
De reden is dat gekeken wordt naar wat het aantal stemmen per zetels is als er een extra zetel wordt toegekend. Bij partijen met veel zetels is de relatieve toename van de extra zetel kleiner en daardoor is de daling van het aantal stemmen per zetel ook kleiner. Hieronder probeer ik dit te illusteren. Let’s get technical!
In plaats van over een concreet aantal stemmen (S) te praten gebruik ik het aantal kiesdelers dat een lijst haalt. Je kan het vermenigvuldigen met het aantal stemmen per kiesdeler om tot het aantal stemmen te komen. Omdat het aantal stemmen er toch wat natuurlijker uit ziet heb ik het wel in de figuren gezet, in italic, voor een kiesdeler van 1000.
In Figuur 1 staat de verdeling van het volle aantal zetels. Dit is duidelijk trapsgewijs: zowel een partij met 1x de kiesdeler of 1.9x de kiesdeler haalt slechts 1 zetel.
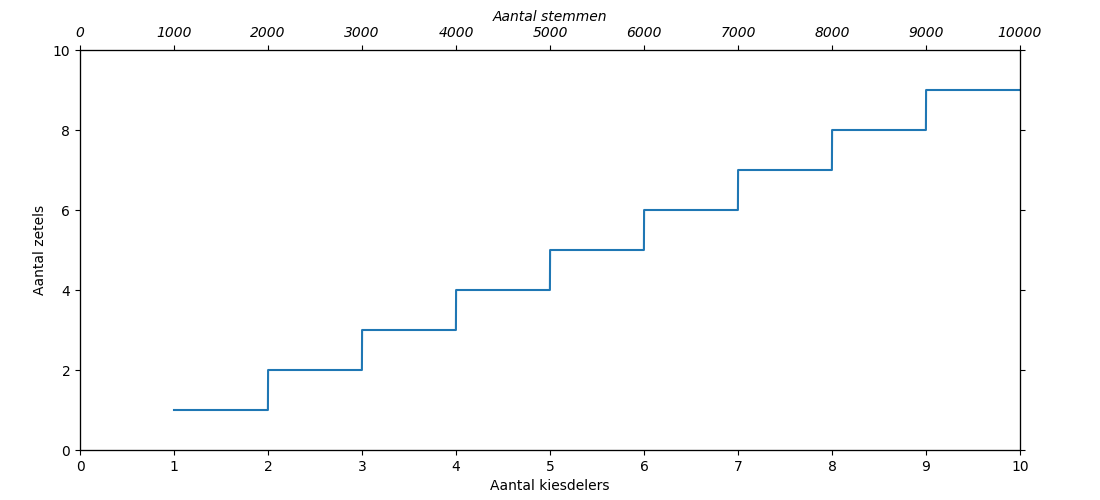
Figuur 1: De verdeling van volle zetels
In Figuur 2 staat het aantal kiesdelers per volle zetel. Dat getal is altijd gelijk aan of groter dan 1. De zaagtand komt doordat het aantal kiesdelers per volle zetel daalt als er een extra virtuele zetel wordt toegekend. Bij 1.99x de kiesdeler wordt 1 zetel toegekend. Het aantal kiesdelers per zetel is dan 1.99. Bij 2.00x kiesdeler worden 2 zetels toegekend. Daardoor daalt het aantal kiesdelers per zetel weer naar 1.00. Bij 2.99 keer de kiesdeler is het aantal kiesdelers per zetel 1.495 (2.99 kiesdelers/2 zetels). Bij 3.00x kiesdelers daalt het weer naar 1. Bij 9.99x kiesdeler is het aantal kiesdelers per zetel 1.11 (9.99 kiesdelers/9 zetels). Het is duidelijk dat het aantal kiesdelers per volle zetel heel sterk fluctueert voor lijsten met weinig kiesdelers (stemmen) en veel minder voor lijsten met veel kiesdelers.
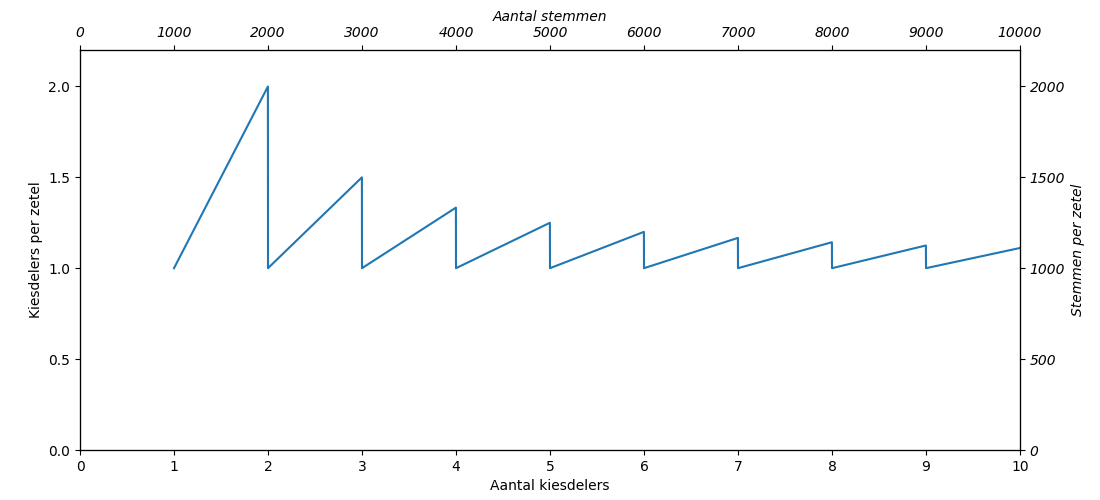
Figuur 2: Het aantal kiesdelers per volle zetel
Om de restzetels toe te kennen worden er extra zetels toegekend. De echte zetels plus extra zetels heten virtuele zetels. Hiermee wordt het aantal kiesdelers per virtuele zetel uitgerekend. Figuur 3 laat dit zien voor 1, 2, 3 en 4 extra zetels.
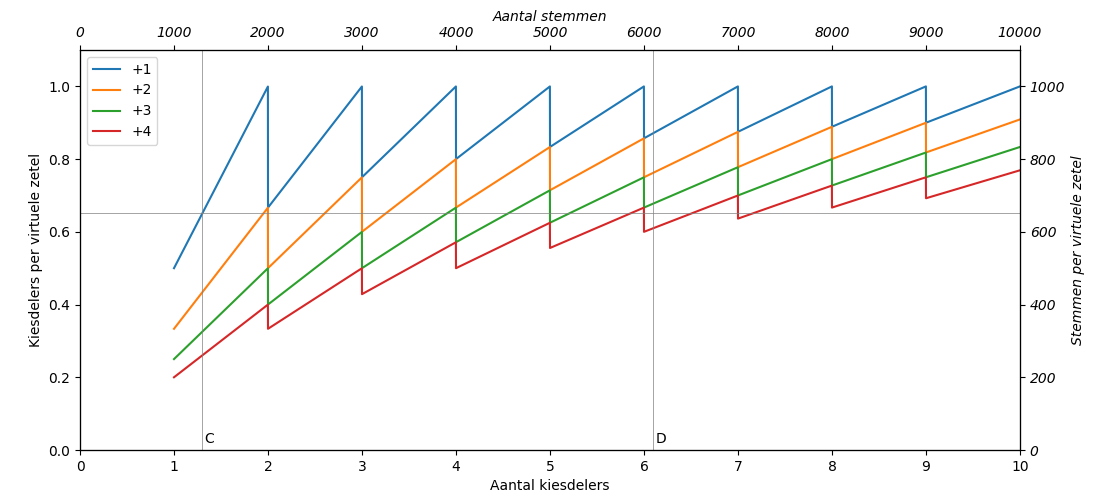
Figuur 3: Het aantal kiesdelers per virtuele zetel. De verticale lijnen zijn het aantal kiesdelers die partijen C en D hebben gehaald, in het voorbeeld in de tekst. De grijze horizontale lijn is het aantal kiesdelers per virtuele zetels voor partij C met 1 extra zetel.
De restzetels worden één voor één toegekend. Eerst wordt bij elke partij 1 extra zetel opgeteld en het aantal kiesdelers per virtuele zetels berekend, dit is de blauwe lijn. Laten we als voorbeeld partijen C en D nemen. Partij C heeft 1.3x kiesdeler en heeft dus 2 virtuele zetels (1 echte en 1 extra) en komt op 0.65 kiesdelers/virtuele zetels (dit staat aangegeven met een horizontale grijze lijn in Figuur 3). Partij D met 6.1x de kiesdeler heeft (6+1=) 7 virtuele zetels en heeft heeft 0.87 kiesdelers per virtuele zetel (waar de vertical grijze lijn van D de blauwe lijn kruist). D heeft dus een hoger gemiddelde dan C (het is boven de horizontale grijze lijn) en de eerste restzetel wordt dus aan partij D worden toegekend.
Voor een tweede restzetel wordt voor partij D het aantal kiesdelers per virtuele zetel opnieuw berekend, nu voor (7+1=) 8 virtuele zetels (de oranje lijn). Voor partij C veranderd er niets en kijken we dus nog steeds naar de blauwe lijn. Partij D heeft in dit geval 0.76 kiesdelers per virtuele zetel, weer meer dan partij C. De tweede restzetel wordt dus ook aan partij D toegekend.
Voor een derde restzetel kunnen we deze exercitie herhalen. Partij D heeft met 3 extra zetels 0.68 kiesdelers per virtuele zetel (groene lijn) en de derde restzetel zal dus ook naar partij D gaan. Pas bij een vierde restzetel daalt het aantal kiesdelers per virtuele zetel voor partij D tot 0.61 (rode lijn) en zou de zetel dus aan partij C worden toegekend.
Uit Figuur 3 en het voorbeeld hierboven blijkt wel dat kleine partijen een nadeel hebben bij het verdelen van restzetels. Het is eigenlijk alleen mogelijk als ze bijna een extra zetel hadden gehaald. Hoe meer zetels een partij haalt, hoe minder het gemiddelde daalt als er extra zetels worden toegekend. Figuur 4 laat hetzelfde zien als Figuur 3, maar dan voor een groter aantal kiesdelers.
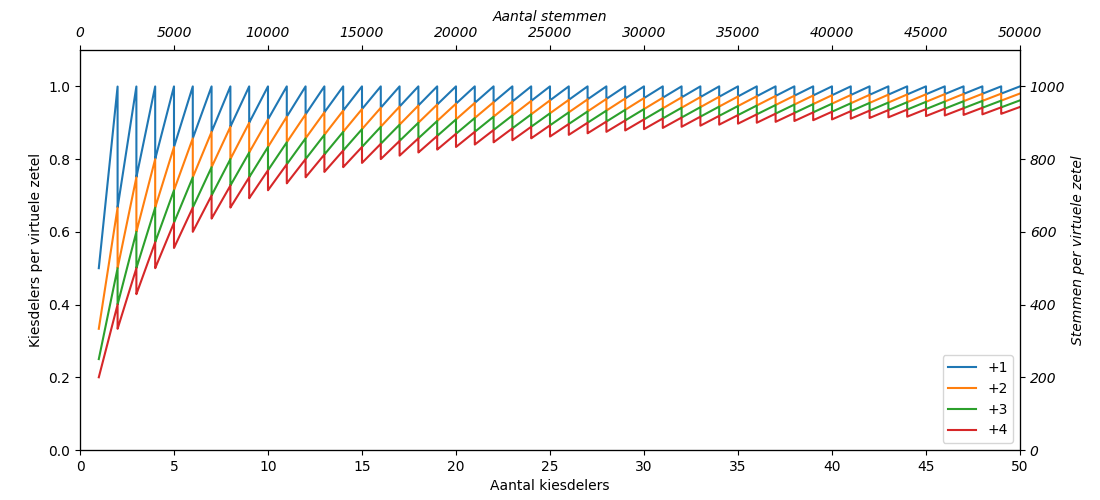
Figuur 4: Het aantal kiesdelers per virtuele zetel
In Figuren 3 en 4 gaan het over het aantal keer de kiesdeler en daar zit een maximum aan: het aantal zetels. Als er 19 zetels zijn dan kan een partij maximaal 19 keer de kiesdeler aan stemmen halen (als ze alle stemmen halen, in welk geval restzetels geen issue meer zijn). In de Tweede Kamer zijn er maximaal 150 kiesdelers te halen. Partijen kunnen dus 30, 40 of zelfs 50 keer de kiesdeler halen. Gemeenteraden hebben tussen de 9 en 45 zetels, afhankelijk van hoe groot de gemeente is. De sterke fluctuaties zijn de reden dat voor kleinere gemeenteraden (minder dan 19 zetels) een ander systeem wordt gebruikt. Toch zullen ook in grotere gemeenteraden de partijen relatief klein zijn.
Voor de volledigheid het systeem met grootste overschotten. Figuur 5 laat zien hoe de overschotten fluctueren voor het aantal kiesdelers. De toewijzing van restzetels is dus onafhankelijk van het aan kiesdelers dat behaald is.
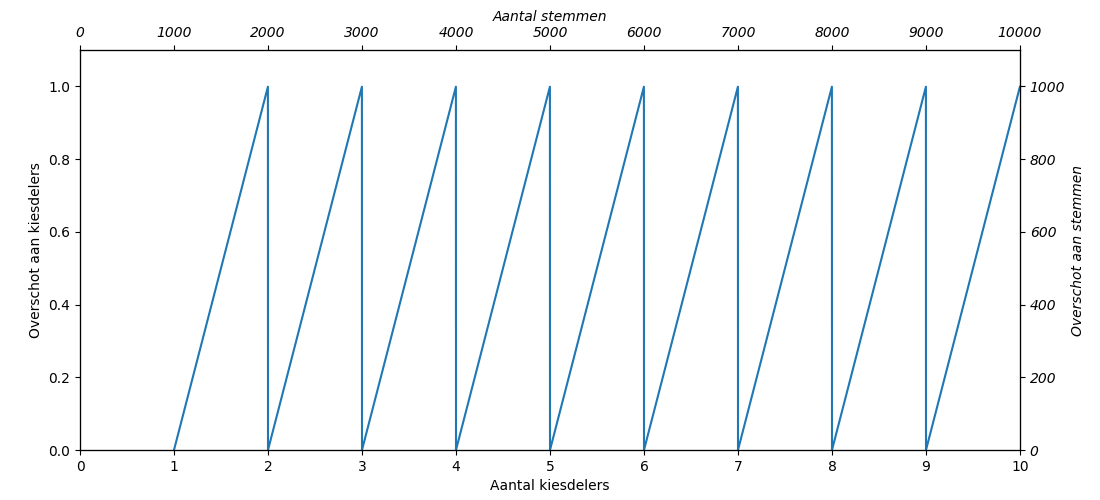
Figuur 5: Overschot aan kiesdelers
Lijstverbindingen
Met een lijstverbinding konden twee of meer partijen hun lijsten samenvoegen en profiteren van het voordeel van het hebben van meer kiesdelers (stemmen), zoals hierboven besproken. De CU en SGP deden dit vaak, net als de PvdA, GroenLinks en SP (soms met z’n tweeën, soms met z’n drieën). Binnen een lijstverbinding worden de zetels dan verdeeld met een lijstkiesdeler en het systeem van grootste overschotten voor restzetels. Een belangrijke voorwaarde was dat partijen in een lijstverbinding individueel in ieder geval één zetel zouden moeten hebben gehaald. In 2017 zijn lijstverbindingen afgeschaft.
Verschillen tussen verkiezingen
Bij de Tweede Kamer en Europese verkiezingen komen alleen partijen die de kiesdrempel hebben gehaald in aanmerking voor restzetels. Bij verkiezingen voor gemeenteraden met minder dan 19 zetels komen alleen partijen die 75% of meer dan de kiesdeler hebben gehaald in aanmerking voor restzetels.